Lessons

Remainders theorem – Euler’s – Carmichael’s Theorem

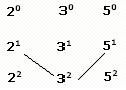
Remainder Theorems

Remainders-CAT-MAT-GMAT

It is uncanny how children pick up a lot of small habits and beliefs of their parents. Even the ones that rebel against their parents bear the subconscious resemblance to their father or mother. There is a lesson for instructors in this. It is important for them to realize that students mirror their feelings about CAT. If the instructor expresses or feels that CAT is tough, or is fearful about CAT, his students will mirror the same feeling and will be less confident. If the instructor is brazen and casual about the paper and scoffs the competition, his students would reflect the same feelings. Also, it is so necessary to have unflinching faith in one’s students. I still remember that during my school days my mother used to proudly proclaim that I was an intelligent kid. I was barely scrapping passing marks in the school exams. If truth be told I was at the bottom of the class, but my mother had her blinkers on. And because of my mother, I also believed that I was second to none. It was only years later, during my boards exams, that I took to studying seriously, and managed to outperform everyone else. I don’t know if it was my mother’s blind love for me or that she could see some bright spark in me that made her claim my intelligence but it really had great effect on my attitude. And attitude, in an exam like CAT, is everything.

Well, it’s almost everything. A keen attitude towards CAT subjects’ fundamentals also plays an important role in one’s performance.

Read More

Counting In Geometry!

Counting in Geometry


(a) In a plane, if there are n points of which no three are collinear, then

  1. The number of straight lines that can be formed by joining them is nC2.
  2. The number of triangles that can be formed by joining them is nC3.
  3. The number of polygons with k sides that can be formed by joining them is nCk.

(b) In a plane, if there are n points out of which m points are collinear, then

  1. The number of straight lines that can be formed by joining them is nC2 – mC2 + 1.
  2. The number of triangles that can be formed by joining them is nC3 – mC3.
  3. The number of polygons with k sides that can be formed by joining them is nCk – mCk.

(c) The number of diagonals of an n sided polygon is nC2 – n = n × (n – 3)/2

Read More

Last two digits of a number ( Method of finding Last two digits)

Last two digit
Last two digits

I am dividing this method into four parts and we will discuss each part one by one:

a. Last two digits of numbers which end in one
b. Last two digits of numbers which end in 3, 7 and 9
c. Last two digits of numbers which end in 2
d. Last two digits of numbers which end in 4, 6 and 8

Before we start, let me mention binomial theorem in brief as we will need it for our calculations.

Last two digit
Binomial theorem

Last two digits of numbers ending in 1

Let’s start with an example.

What are the last two digits of 31786?

Read More

Some Basic Calculation Techniques in Maths

Calculation Techniques

The rules of business can be applied to any competitive environment. Just as businesses keep trying to achieve an extra edge and sell more and more products so do students preparing for competitive exams such as CAT 2018. The focus should always be on trying to achieve more and more. For CAT aspirants, this is the golden rule- always be focused on your goal. That means giving away all your distractions: that movie which other friends are going to watch, those phone calls, whatsapp, facebook, or twitter, those sms, those days of boredom when you do not want to study, and so much more. For every second, minute, hour or day that you lose, someone is trying to get ahead of you. The fact is that you are not going to become a CAT cracker overnight; you will have to grow inch by inch. And the other fact is that it is easier to increase your percentile to 95 or 97 from 70 or 80 percentile but it is much much tougher to increase it further to 99+. So the more you are at the top, the harder it is to grow further. And it takes focus and dedication climb day by day.

I am very fond of today’s chapter. These tricks are used by me off an on and I teach them in my first class also. The result is that all my students are able to work out calculations mentally by the end of the class. The sad fact is that they do not continue it once they get home, which is a pity. If they keep up the practise for 3 or 4 months, they would see themselves doing wonders, as I saw with myself. But practicing it day in and day out again takes focus and vision of one’s goal.

Read More

last non zero digit of factorial -TG Math Corner

last non zero digit

At every step in life, we face diverse problems. They may be related to our family, health, education, career and much more. There can be no one who says that I never had a problem. Srimad Bhagwatam [10.14.58] says ‘padam padam yad vipadam’ which means that at every step in life we face problems. Now how to eradicate our problems is the biggest problem. One thing is sure that we cannot escape the discomfort created because of the problems of life. So the wiser advice will be to find out the root cause of our problems and try to kill it. And remember, we must help each other by solving each other’s problems. That makes life smoother. You get dependable and caring friends which you’d like to carry along throughout life.

Coming back to our math worries, many students have repeatedly asked us to create a Quant corner where we can post our (beautiful) solutions to beautiful math problems and discuss some small concepts. So here we are! This place is open for discussions as that is the best way of learning. So let’s start today’s mathematical extravaganza.

Read More

Average -Mixture and Alligation For CAT 2018 students

Average mixture
Average mixture

 

The concept of averages is hardly a new concept at all. If asked, all of you would give me the following formula for calculating

Average mixture
Average formula

 

 

 

So far so good. But if I ask all of you to solve a simple problem many of you would reach for their pens.

The average score of three students A, B, and C is 50. When the score of another student D is added to the group, the average score becomes 47. What is the score of student D?

Answer: for most of you, the score of student D would be 4 × 47 – 3 × 50 = 38.

For me, the calculation would just be 47 – 9 = 38.

Some of you might have understood what I did. Let me start explaining through a simple example. Then we shall extend our explorations to more complex problems.

Read More

Divisors of a Number ( Number of Divisors of a number)

How do we find divisors of a number? For example, how do we calculate the number of divisors of 900?

Answer: 900 = 22 × 32 × 52. Therefore, any number that is a factor of 900 can have powers of 2 equal to 20, 21 or 22. Similarly, for 3, the powers can be 30, 31, or 32 and for 5 they will be 50, 51, or 52. Writing the powers in a line we have-

Divisors of a Number

Now any combination of a power of 2, a power of 3, and a power of 5 will give us a divisor. For example, in the figure, 21 × 32 × 51 will be a divisor of 900. As we can select a power of 2 in 3 ways, a power of 3 in 3 ways, and a power of 5 in 3 ways, the total number of combinations will be 3 × 3 × 3 = 27. Therefore, the number of divisors of 900 is 27.

Read More